[Paper Review] Denoising Diffusion Probabilistic Models

Paper Review

제목 : Denoising Diffusion Probabilistic Models
저널 : NeurIPS
저자 : Jonathan Ho, Ajay Jain, Pieter Abbeel
일시 : 16 Dec 2020
연구 : UC Berkeley

 

해당 논문 리뷰는 위 출처의 논문을 리뷰한 것입니다.

 

오류나 내용 정정 요청에 대한 문의는 언제나 환영입니다.

 

본 논문 리뷰를 읽기 전 꼭 아래 background를 먼저 숙지하시기 바랍니다.

 

< Summary & Contributions >

1. data에 random noise를 더해준 후 noise를 제거하는 과정을 학습하는 모델

2. forward process : data에 noise를 추가하는 과정으로 markov chain을 통해 gradually noise를 더해 나감

3. reverse process : Gaussian noise에서 시작하여 gradually noise를 제거하는 과정

 

 

image generation이란 무엇일까?

 

사용자가 원하는 이미지를 얻어내는 것이다.

 

결국 우리는 우리가 원하는 data의 distribution을 얻어내는 것이다.

 

해당 distribution은 특정한 maniford를 따른다.

 

그것이 곧 우리가 probabilistic genertive modeling을 한다고 볼 수 있다.

 

그 분포를 알아내는 모델을 만드는 것이다.

 

 

그렇다면 여기서 사용되는 함수를 f라고 하자.

 

latent vector z가 있다고 했을 때,

 

z를 f에 넣으면 원하는 data가 나오는 것이다.

 

그 과정에서 우리는 그저 noise한 latent vector z에서 원하는 결과를 얻어내도록 한다.

 

이것은 VAE, GAN, Normalizling flow, diffusion models을 거쳐

 

2021년부터 많은 diffusion 붐을 이뤄온

 

DDPM에 도달하게 된 배경이다. 

 

 

 

Background

 

1. nonequilibrium thermodynamics

• 불균형 열역학이라고 합니다.
• nonequilibrium thermodynamics은 물리학에서의 확산과 열역학에 대한 개념입니다.
• 확산 과정 : 확산의 원리와 Brownian motion 등의 개념
• 열역학 : 열역학의 법칙, 특히 nonequilibrium 상태에 대한 개념

 

 

2. Diffusion Probabilistic Models (Jihye Back님 blog 발췌 내용입니다. 출처는 글 하단에 있습니다.)

• 딥러닝에서 현실의 복잡한 dataset을 probability distribution으로 표현하는 것은 매우 중요하다.
• 특히 우리가 이 probability distribution을 구하고자 할 때, tractability와 flexibility라는 개념이 중요한데, 이는 서로 trade-off 관계에 있기 때문에 이 둘을 동시에 만족하긴 어렵다. (복잡한 data에 대해서도 잘 fitting 되어 있으면서도 계산이 용이한 분포를 찾기 어려움)

 

Diffusion Probability Model

1. extreme flexibility in model structure
2. exact sampling
3. easy multiplication with other distributions, e.g. in order to compute a posterior, and
4. the model log likelihood, and the probability of individual states, to be cheaply evaluate

 

초창기 Diffusion Probability Model(2015)에서는 diffusion 과정을 통해 우리가 잘 알고있는 distribution (ex. Gaussian)을 target data distribution으로 변환해주는 markov chain을 학습시켜 flexible하면서도 tractable한 distribution을 구하고자 하였다.

 

 

 

3. Latent Variable Models

 

잠재 변수 모델 (Latent Variable Models, LVMs)은 관측 데이터의 생성 과정 뒤에 숨겨진 변수, 즉 'latent variable'이 있다고 가정하는 통계 모델입니다. 이런 모델에서 latent variable은 직접적으로 관측되지 않지만 관측 데이터의 분포나 구조에 영향을 준다고 가정됩니다.

 

LVMs의 주요 장점은 복잡한 데이터 구조를 단순화하여 모델링할 수 있다는 것입니다. 예를 들어, 고차원의 데이터를 저차원의 latent space에 투영하면 데이터의 주요 패턴이나 구조를 효과적으로 포착할 수 있습니다.

효과적인 LVM 예로는 다음과 같은 것들이 있습니다:

• PCA (주성분 분석): 데이터의 분산을 최대화하는 축을 찾아 데이터를 저차원으로 투영합니다.
• Factor Analysis: 관측 데이터의 분산과 공분산 구조를 설명하기 위해 잠재 변수를 도입합니다.
• Variational Autoencoders (VAEs): 딥 러닝과 잠재 변수 모델링을 결합하여 데이터의 복잡한 분포를 학습합니다.

이러한 모델들은 데이터의 복잡한 분포나 구조를 간소화하여 표현하고, 데이터 생성, 클러스터링, 차원 축소 등 다양한 문제를 해결하는 데 사용됩니다.

 

 

 

 

 

본 논문에서는 diffusion probabilistic models을 사용하여 high quality image synthesis results를 내며,

 

여기서 diffusion probabilsitic models은 nonequilibrium thermodynamics에 영감을 받은 latent variable models(LVMs)의 한 종류입니다.

 

best results는 diffusion probabilistic models과 Langevin dynamics를 사용한 denoising score matching 간의 새로운 연결에 따라 설계된 weighted variational bound에서 학습함으로써 얻어졌습니다.

 

그리고, 본 모델은 자연스럽게 autoregressive decoding의 일반화로 해석될 수 있는 progressive lossy decompression schme을 채택합니다.

 

unconditional CIFAT-10 dataset에서 본 모델은 Inception score 9.46과 highest FID score 3.17을 얻었습니다.

 

256 x 256 LSUN에서는 ProgressiveGAN과 유사한 sample quality를 얻었습니다.

 

 

 

Introduction

 

• GANs, Autoregressive models, Normalizing flows, variational autoencoders(VAEs)는 striking image, audio samples를 합성하며 energy-based modeling과 score matching 에 있어 놀라운 진보를 이끌어냈습니다.

 

• 한편, 본 논문에서는 diffusion probabilistic models의 진보를 나타냅니다.

 

• Diffusion probabilistic models은 parameterized Markov chain으로 유한한 시간 후 데이터와 일치하는 Sample을 생성하기 위해 variational inference를 사용하여 학습됩니다.

 

• 이 chain의 transition은 diffusion process를 reverse시키도록 학습되는데, 이 diffusion process는 data에 점진적으로 noise를 추가하는 Markov chain으로, sampling의 반대 방향으로 signal이 파괴될 때까지 계속됩니다.

 

• diffusion이 작은 양의 Gaussian noise로 이루어질 때, sampling chain transition을 conditional gaussian으로 설정하는 것이 충분하며, 특히 단순한 neural network parameterization을 허용합니다.

 

 

 

Figure 2 : The directed graphical model considered in this work

 

 

• diffusion models은 간단하게 정의되며 효과적으로 학습될 수 있지만, high quality samples을 생성할 수 있는 능력에 대한 명확한 증거는 제시되지 않았습니다.

 

• 본 논문에서 저자들은 diffusion models이 실제로 high quality samples을 생생할 수 있으며, 때로는 다른 generative models에 대한 발표된 결과보다 더 우수한 결과를 얻을 수 있다는 것을 보여줍니다.

 

• 추가적으로 diffusion models의 특정한 방식의 구성은, Training 중 multi noise level에 대한 denoising scroe matching과 sampling 과정 중 annealed Langevin dynamics과 같다는 것을 보여줍니다.

 

• 본 논문에서 이러한 구성 방식을 사용하여 best sample quality results를 얻었고, 이러한 동등성은 본 연구의 주요 contribution 중 하나로 간주합니다.

 

• sample quality에도 불구하고, diffusion models은 다른 log likelihood 기반의 모델들과 비교했을 때 경쟁력 있는 log likelihood를 갖지 않습니다.

 

• 그러나, diffusion models의 log likelihood는 energy based models과 score matching에 대해 보고된 큰 추정치보다는 더 나은 결과를 보였습니다.

 

• diffusion models 대부분의  lossless codelengths는 감지하기 어려운 image details를 기술하는 데 사용됩니다.

 

• 본 논문의 저자들은 lossy compression의 언어로 이 현상에 대한 더 정밀한 분석을 제시하고, diffusion models의 sampling 절차가 일반적으로 autoregressive models로 가능한 것을 크게 확장하는 방식의 progressive decoding이라는 것을 보여줍니다.

 

 

Background Formula

 

Diffusion models은 $ p_\theta(x_0) = \Sigma p_\theta (x_{0:T}) d_{x_{1:T}} $의 형태를 가지는 latenet variable models의 일종으로 data $  x_1, ..., x_T $ 는 $ x_0 ~ q(x_0) $ 와 같은 dimensionality를 가지는 형태로 주어집니다.

 

Joint distribution $ p_\theta(x_{0:T}) $ 는 reverse process이라 하며,

 

이는 learned Gaussian transition을 가진 Markov Chain의 형태로 정의 됩니다.

 

이 chain은 $ p(x_T) = \mathcal{N}(x_{t-1}; 0, I) $ 에서 시작합니다.

 

diffusion models이 다른 종류의 latent variable models과 구별되는 점은,

 

forward process or diffusion process이라고 불리는 approximate posterior $ q(x_{1:T }| x_0) $ 가 분산 일정 $ \beta_1, ..., \beta_T $에 따라 data에 gaussian noise를 점진적으로 추가하는 Markcov chain에 고정된다는 것입니다.

Training은 negative log likelihood에 대한 일반적인 variational bound를 최적화함으로써 수행됩니다.

 

 

 

forward process variances $ \beta_t $는 reparameterization를 통해 학습될 수 있거나 상수로 유지될 수 있습니다.

 

reverse process의 expressiveness는 $ p_\theta(x_{t-1}|x_t)에서 Gaussian conditionals의 선택에 의해 부분적으로 보장됩니다.

 

왜냐하면 $ \beta_t $가 작을 때 두 과정 모두 동일한 함수 형태를 갖기 때문입니다.

 

forward process의 주목할만한 특성은 임의의 timestep t에서 $ x_t $ sampling을 closed 상태로 허용한다는 것입니다.

 

: 표기법 $ \alpha_t = 1 - \beta_t $ 와 $ \bar{\alpha}_t = \prod\nolimits_{s=1}^t \alpha_s$ 를 사용하여, 다음의 결과를 얻습니다.

 

 

효과적인 Training은 stochastic gradient descent를 사용하여 L의 무작위 항목들을 최적화함으로써 가능합니다.

 

더 나아가 L(3) 을 다음과 같이 재작성 함으로써 variance reduction의 개선이 이루어집니다.

 

 

위 수식은 KL divergence를 사용하여 $ x_0 $에 조건을 부여했을 때 처리 가능한 forward process posteriors 에 대해 $ p_\theta(x_{t-1}|x_t)를 직접 비교합니다.

 

 

결과적으로, Eq.(5)의 모든 KL Divergence는 Gaussian 간의 비교이므로, high variance Monte Carlo estimates 대신 closed form의 표현식으로 Rao-Blackwellized 방식으로 계산할 수 있습니다.

 

 

 

 

Diffusion models and denoising autoencoders

 

diffusion models은 variable models의 제한된 class처럼 보일 수 있지만, implementation에서 많은 자유도를 허용합니다.

 

forward process의 variance $ \beta_t $와 reverse process의 model architecture 및 gaussian distribution parameterization을 선택해야 합니다.

 

본 선택을 안내하기 위해 Diffusion model과 denoising score matching 간의 새로운 명시적 연결을 확립하고, diffusion models의 간단하고 Weighted variational bound objective를 도출합니다.

 

결국, 본 diffusion models 설계는 단순함과 실제 결과에 의해 정당화됩니다.

 

아래 논의는 Eq.(5)의 용어로 분류됩니다.

 

Forward process and $ L_T $

 

본 논문에서 forward process의 variance $ \beta_t $ 가 reparameterization으로 학습 가능하다는 사실을 무시하고 대신 constant로 고정합니다. 따라서, 본 구현에서는 approximate posterior q에 learnable parameters가 없으므로, $ L_T $ 는 훈련 중에 constant이며 무시할 수 있습니다.

 

Reverse process and $ L_{1:T-1} $

 

$ 1 < t \leq T $ 에 대해 $ p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t)) $에서 본 저자들의 선택을 논의합니다.

 

먼저, $ \Sigma_\theta(x_T, t) = \sigma_t^2I $ 를 untrained time dependent constants로 설정합니다.

 

실험적으로, $ \sigma_t^2 = \beta_t $ 와 $ \sigma_t^2 = \tilde{\beta}_t = \frac{1 - \tilde{\alpha}_{t-1}}{1-\tilde{\alpha}_t}\beta_t $의 결과는 유사했습니다.

 

첫 번째 선택은 $ x_0 ~ \mathcal{N}(0,I) $에 최적이며, 두 번째는 $ x_0 $를 결정론적으로 하나의 포인트로 설정하는 경우에 최적입니다.

 

이것은 coordinatewise unit variance를 가진 데이터에 대한 reverse process entropy의 upper과 lower에 해당하는 두 가지 극단적인 선택입니다.

 

 

 

두 번째로,

 

평균 $ \mu_\theta(x_t, t) $ 를 나타내기 위해 $ L_t $의 분석에 기반한 specific parameterization을 제안합니다.

 

 

$ p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2I) $와 함께, 다음과 같이 쓸 수 있습니다.

 

그리고 여기 C는 상수로 $ \theta $에 의존하지 않습니다.

 

따라서, $ \mu_\theta $에 가장 직관적인 parameterization은 forward process posterior mean인 $ \tilde{\mu}_t $를 예측하는 models임을 알 수 있습니다.

 

그러나, Eq.(4)를 $ x_t(x_0, \epsilon) = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha_t}} \epsilon$ 으로 reparameterization하여 Eq.(8)를 더 확장할 수 있습니다.

 

여기서$ \epsilon $은$ \mathcal{N}(0 ,I) $를 따릅니다.

 

그리고 forward process posterior formula(7)을 적용합니다.

 

 

 

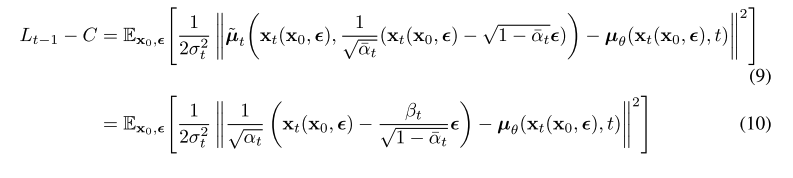
위 Eq.(10)은 $ \mu_\theta $가 반드시 $ x_t $가 주어졌을 때,  $ \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_t}}\epsilon) $ 를 예측해야 한다는 것을 나타냅니다.

 

$ x_t $는 model의 input으로 이용가능하기에, 아래와 같이 parameterization을 선택합니다:

 

 

여기서 $ \epsilon_\theta $는 $ x_t $에서 $ \epsilon $을 예측하기 위한 function approximator 입니다.

 

$ x_{t-1} ~ 

 

 

 

 

 

 

 

 

 

< 정리 >

 

 

---

< 본 논문에 대한 본 포스팅 저자의 생각 >

 

해당 내용은 저의 개인적인 의견이니 참고용으로만 바라봐주세요 🌈

 

Diffusion model은 굉장히 많은 분야에 좋은 성능으로 사용되고 있다.

ㅇㅇㅇ

 

 

 

 

Reference

 

 

https://arxiv.org/abs/2006.11239

Denoising Diffusion Probabilistic Models

 

 

https://github.com/lucidrains/denoising-diffusion-pytorch

GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch

 

 

https://arxiv.org/abs/1503.03585

Deep Unsupervised Learning using Nonequilibrium Thermodynamics

https://github.com/Sohl-Dickstein/Diffusion-Probabilistic-Models

GitHub - Sohl-Dickstein/Diffusion-Probabilistic-Models: Reference implementation for Deep Unsupervised Learning using Nonequilib

https://happy-jihye.github.io/diffusion/diffusion-1/

[Paper Review] DDPM: Denoising Diffusion Probabilistic Models 논문 리뷰

https://www.reportworld.co.kr/knowledge/2248

열역학이란?